Profa Márcia/ Alunos nota DEZ
Educar é impregnar de sentido o que fazemos a cada instante! Paulo Freire
quinta-feira, 5 de fevereiro de 2026
sexta-feira, 8 de agosto de 2025
COMPARAÇÃO DE FRAÇÃO
Comparar frações significa olhar para duas frações e descobrir qual é a maior. Para comparar frações, tudo o que precisa fazer é deixá-las com o mesmo denominador e ver qual tem o maior numerador, assim você dirá qual é maior. A parte mais difícil é saber como ter certeza que as frações têm denominadores comuns, mas não é tão complicado assim. Se quiser saber como comparar frações, siga os Passos abaixo.

1º passo Veja se as frações têm os mesmos denominadores. Esse é o primeiro passo para compará-las. O denominador é o número de baixo da fração e o numerador, o de cima. Por exemplo, as frações 5/7 e 9/13 não têm o mesmo denominador porque 7 não é igual a 13. Dessa forma, você precisar fazer algumas coisas para compará-las.
- Se o denominador das frações for o mesmo, você só precisa olhar o numerador para saber qual é maior. Por exemplo, com as frações 5/12 e 7/12, você sabe que 7/12 é maior que 5/12 porque 7 é maior que 5.

- 7 x 13 = 91, portanto o denominador comum entre essas duas frações será 91

- 3º Passo Altere os numeradores das frações. Agora, você precisará alterar os numeradores para que os valores das frações continuem os mesmos. Para fazer isso, você precisará multiplicar o numerador de cada fração pelo mesmo número que multiplicou o denominador para chegar a 91.
- Com a fração original 5/7, você multiplicou 7 por 13 para chegar no denominador 91, portanto precisará multiplicar 5 por 13 para ter o novo numerador. Basicamente, você estará multiplicando o numerador e o denominador da fração por 13/13 (que é igual a 1). 5/7 x 13/13 = 65/91.
- Com a fração original 9/13, você multiplicou 13 por 7 para chegar no denominador 91, portanto precisará multiplicar 9 por 7 para ter o novo numerador. 9 x 7 = 63, portanto a nova fração é 63/91.

COMO ENCONTRAR FRAÇÕES EQUIVALENTES
Como encontrar frações equivalentes.
Temos duas maneiras se checar se frações são equivalentes
entre si sem precisar desenhar que já vimos na nossa apostila.
Um é através da multiplicação e o outro é pela divisão.
Como Calcular o MMC.
O cálculo do MMC, pode ser feito, através da comparação da tabuada desses números. Por exemplo, vamos descobrir o MMC de 2 e 3. Para isso, vamos comparar a tabuada de 2 e 3:
Note que o menor múltiplo em comum é o número 6. Portanto, dizemos que o 6 é o mínimo múltiplo comum (MMC) de 2 e 3.
Essa forma de encontrar o MMC é bem direta, mas quando temos números maiores ou mais de dois números, não é muito prática.
Para essas situações, o melhor é usar o método da fatoração, ou seja, decompor os números em fatores primos. Acompanhe, no exemplo abaixo, como calcular o MMC entre 12 e 45 usando esse método:
Mínimo Múltiplo Comum e Frações
O mínimo múltiplo comum (MMC) é também muito utilizado em operações com frações. Sabemos que para somar ou subtrair frações é necessário que os denominadores sejam iguais.
Assim, calculamos o MMC entre os denominadores, e este passará a ser o novo denominador das frações.
Vejamos abaixo um exemplo:
Como os denominadores são diferentes, o primeiro passo é encontrar o MMC entre 5 e 6. Fatorando, temos:

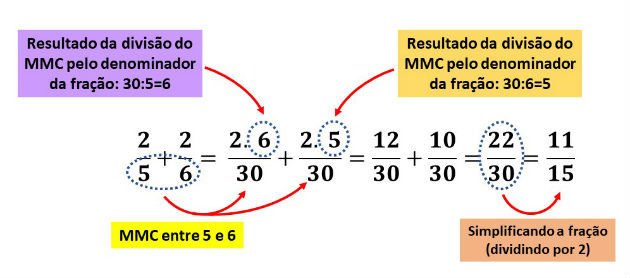
Agora que já sabemos que o MMC entre 5 e 6 é 30, podemos efetuar a soma, fazendo as seguintes operações, conforme indicado no diagrama abaixo:
Agora que já sabemos que o MMC entre 5 e 6 é 30, podemos efetuar a soma, fazendo as seguintes operações, conforme indicado no diagrama abaixo:
quarta-feira, 6 de agosto de 2025
Expressões Matemáticas com Passo a Passo
Expressões Matemáticas com Passo a Passo
Ordem das Operações – Regra PEMDAS
O que é PEMDAS?
PEMDAS é uma sigla que nos ajuda a lembrar da ordem correta das operações matemáticas:
P – Parênteses: resolva primeiro o que está dentro dos parênteses.
E – Expoentes: calcule as potências (como 22, 33).
MD – Multiplicação e Divisão: da esquerda para a direita.
AS – Adição e Subtração: também da esquerda para a direita.
■ Dica: quando multiplicação e divisão aparecem juntas, resolva na ordem em que aparecem da
esquerda para a direita. O mesmo vale para adição e subtração.
Seguir essa ordem evita erros e garante que todos cheguem ao mesmo resultado!
1a Expressão:
(15 × 8) - 4 × 4 + 15
Passo 1: Parênteses
15 × 8 = 120
Substituindo: 120 - 4 × 4 + 15
Passo 2: Multiplicação
4 × 4 = 16
Substituindo: 120 - 16 + 15
Passo 3: Subtração e Adição da Esquerda para a Direita
120 - 16 = 104
104 + 15 = 119
Resultado final: 119
2a Expressão (corrigida):
7 - 2 × 3 + (2 × 4 + 7)
Passo 1: Parênteses
2 × 4 = 8
8 + 7 = 15
Substituindo: 7 - 2 × 3 + 15
Passo 2: Multiplicação
2 × 3 = 6
Substituindo: 7 - 6 + 15
Passo 3: Subtração e Adição da Esquerda para a Direita
7 - 6 = 1
1 + 15 = 16
Resultado final: 16
segunda-feira, 19 de maio de 2025
COMPRIMENTO
O decâmetro (dam), o hectômetro (hm) e quilômetro (km) são maiores que o metro, e são classificadas como múltiplos do metro.
O decímetro (dm), o centímetro (cm) e o milímetro (mm) são menores que o metro, e são classificadas como submúltiplos do metro.
O metro é considerado a medida de comprimento referencial. Observe a relação demonstrada na tabela:
sexta-feira, 11 de abril de 2025
Conversão de medidas
O decâmetro (dam), o hectômetro (hm) e quilômetro (km) são maiores que o metro, e são classificadas como múltiplos do metro.
O decímetro (dm), o centímetro (cm) e o milímetro (mm) são menores que o metro, e são classificadas como submúltiplos do metro.
O metro é considerado a medida de comprimento referencial. Observe a relação demonstrada na tabela:
-
Para fazer a leitura de números muito grandes, dividimos os algarismos do número em classes (blocos de 3 ordens), colocando um ponto para se...
-
REVISÃO DE MATEMÁTICA Olá galerinha! Para fazer a leitura de números muito grandes, dividimos os algarismos do número em classe...
-
Olá! Galerinha! Vamos estudar um pouquinho de história! Década – corresponde a um período de 10 anos, começa sempre com um ano com...






















