Operações com números decimais

Nomenclatura de números decimais

A fim de facilitar as definições que virão, a seguir estabelecemos algumas nomenclaturas. Um número decimal é formado por sua parte inteira e pela parte decimal. A parte decimal é organizada da seguinte maneira: décimo, centésimo, milésimo, décimo de milésimo, centésimo de milésimo e assim por diante.

Veja o exemplo:

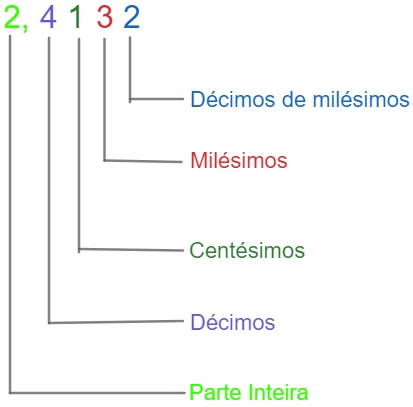
Adição com números decimais

A adição de números decimais é definida de maneira semelhante à adição de números inteiros, nessa operação devemos somar parte inteira com parte inteira, décimos com décimos, centésimos com centésimos, e assim sucessivamente. Em outras palavras, devemos colocar vírgula abaixo de vírgula, veja o exemplo.

Exemplo 1

Vamos determinar a soma dos números 0,65 e 0,792. Lembre-se: o número 0 no final de qualquer número decimal não acresce no valor.

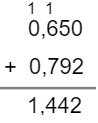
Exemplo 2

Determine o valor da soma 1,442 + 2,4.

As operações com números decimais são indispensáveis para o nosso cotidiano.

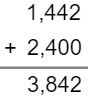
Subtração com números decimais

A subtração entre dois números decimais dá-se do mesmo modo que a sua adição, operamos parte inteira com parte inteira, décimos com décimos, e assim sucessivamente. Veja os exemplos.

Exemplo

Determine a diferença entre os números 3,842 e 1,442.

Multiplicação com números decimais

A multiplicação entre dois números decimais pode ser realizada de duas formas: podemos operar de maneira semelhante à da multiplicação de dois números inteiros, somando, ao final, a quantidade de casas decimais dos dois números e colocando-as no resultado; ou podemos transformar os números decimais em frações e utilizar a multiplicação de fração.

Vamos lembrar como transformar número decimal em fração? Transformação de número decimal para forma fracionária Para escrever um número decimal na sua forma fracionária, devemos conservar o número decimal sem a vírgula no numerador da fração, e no denominador colocamos a potência de 10 de acordo com a quantidade de casas decimais que “andamos” para tornar o número decimal em inteiro. Veja os exemplos. Exemplo 1 Vamos escrever o número 0,43 em forma de fração. Para a vírgula desaparecer, devemos “andar” duas casas decimais, ou seja, precisamos multiplicar o número por 100. Assim: Exemplo 2 Para escrever o número 0,8 na sua forma fracionária, devemos andar uma casa decimal, logo:

Exemplo

Utilizando os dois métodos, determine o produto entre 0,42 e 1,2. Antes de efetuar a multiplicação, perceba que 0,42 possui duas casas decimais e que o número 1,20 possui duas delas. A soma disso resulta em quatro casas decimais, ou seja, o resultado deverá ter quatro casas decimais.

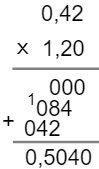
Ou seja 0,42 x 1,2 = 0,504.

Agora, transformando os números para sua forma fracionária, temos a seguinte multiplicação:

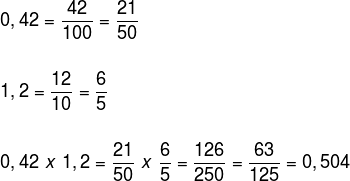
Leia também: Simplificação de fração: aprenda como fazer

Divisão com números decimais

Na divisão de números decimais também vamos observar dois métodos que podem ser considerados equivalentes. O primeiro método consiste em “andar” a mesma quantidade de casas decimais, ou seja, multiplicar por potências de 10 até que a vírgula não esteja mais presente. O segundo método consiste em representar os números em forma de fração e realizar a divisão de frações.

Exemplo

Vamos realizar a divisão entre os números 0,504 e 1,2.

Com o primeiro método, devemos multiplicar o dividendo e o divisor pelo mesmo número até que a vírgula desapareça.

Para que a vírgula desapareça do denominador, devemos multiplicá-lo por 1000, logo, faremos o mesmo com o divisor.

0,504 · 1000 = 504

1,2 · 1000 = 1200

Armando a conta, temos:

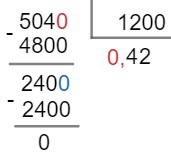
Transformando os números decimais em frações, temos:

 

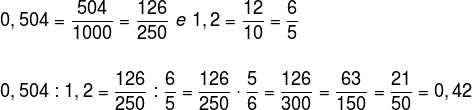
Por Robson Luiz
Professor de Matemática 

Bora lá! Volta às aulas!

MOTIVAÇÃO

 

Multiplicação de frações diretamente

 Felizmente, esse processo é bastante fácil. Se as frações ainda não estiverem em seus menores termos, simplifique-as. A seguir, basta multiplicar um numerador pelo outro e um denominador pelo outro.^[9]

• Para multiplicar ${\displaystyle {\frac {2}{3}}\times {\frac {7}{8}}}$, por exemplo, chegue ao novo numerador multiplicando ${\displaystyle 2\times 7}$, que é igual a ${\displaystyle 14}$, e multiplique ${\displaystyle 3\times 8}$, que resulta em ${\displaystyle 24}$. Desse modo, a resposta será ${\displaystyle {\frac {14}{24}}}$, que pode ser simplificada para ${\displaystyle {\frac {7}{12}}}$ dividindo-se ambos numerador e denominador por ${\displaystyle 2}$.

Divisão de fração

 Divida as frações invertendo a segunda de cabeça para baixo e multiplicando-as a seguir. Na divisão, comece transformando a fração a ser dividida em uma recíproca. Para isso, coloque-a de cabeça para baixo, transformando o numerador em denominador e vice-versa. A seguir, multiplique ambos os valores um pelo outro.^[10]

• Para resolver ${\displaystyle {\frac {1}{2}}\div {\frac {1}{6}}}$, por exemplo, inverta ${\displaystyle {\frac {1}{6}}}$ transformando-a em ${\displaystyle {\frac {6}{1}}}$. A seguir, multiplique ${\displaystyle 1\times 6}$ para chegar ao numerador (que será ${\displaystyle 6}$) e multiplique ${\displaystyle 2\times 1}$ para chegar ao denominador (que será ${\displaystyle 2}$). Desse modo, a resposta obtida será ${\displaystyle {\frac {6}{2}}}$, que é igual a ${\displaystyle 3}$.

OS FERAS DA #rededecisao

Se vocês chegaram até aqui, estimados alunos, e se agora estamos trabalhando juntos, é porque vocês merecem os parabéns. Mas hoje, gostaria de chamar a atenção para uma palavra importante que vocês certamente conhecem: mérito.

Quando uma pessoa conquista alguma coisa com mérito, não é porque ela é inteligente e mais capacitada que os outros à sua volta. Conseguir determinado objetivo com mérito é lutar por ele com todas as forças e, mesmo que seja em dificuldades, não desistir até o alcançar. Afinal, quem vocês acham que teria mais mérito numa prova de corrida, a lebre ou a tartaruga?

Com isto quero dizer que não estou à espera que vocês sejam alunos brilhantes, nem que façam o impossível. Por muitas dificuldades que vocês possam encontrar, não desistam. E, acima de tudo, se esforcem. A maior recompensa que vocês podem ter é chegarem ao final do ano e receberem os resultados sabendo que tiveram todo o mérito neles.

Profa Márcia.

Modos Verbais

Os Modos Verbais (indicativo, subjuntivo e imperativo) indicam as maneiras como os verbos se expressam:

• Indicativo - exprime fatos, certezas. Exemplo: Discursa muito bem.
• Subjuntivo - exprime desejos, possibilidades, dúvidas. Exemplo: Talvez discurse bem esta noite.
• Imperativo - exprime ordens, pedidos. Exemplo: Discurse como ele!

Os modos verbais estão intimamente ligados aos tempos presente, passado e futuro.

Modo Indicativo

O modo indicativo manifesta ações habituais, bem como expressa tanto fatos presentes, como passados ou futuros.

Exemplos:

• Caminho todas as manhãs. (acontece)
• Caminhei ontem à noite. (aconteceu)
• Caminharei sábado à tarde. (acontecerá)

Modo Subjuntivo

O modo subjuntivo manifesta desejos ou hipóteses no tempo presente, bem como no passado e no futuro.

Exemplos:

• Espero que chova durante toda a noite. (desejo presente)
• Se chovesse, as plantas estariam regadas. (hipótese passada)
• Quando chover o caso estará resolvido. (possibilidade futura)

Modo Imperativo

O modo imperativo manifesta ordens ou pedidos de forma afirmativa e também de forma negativa.

Exemplos:

• Ajude a senhora a atravessar a rua. (imperativo afirmativo)
• Não ajude aqueles malandros! (imperativo negativo)

Agora que você aprendeu os modos, saiba tudo sobre Tempos Verbais e Formas Nominais!