REVISÃO DE MATEMÁTICA P2

 REVISÃO DE MATEMÁTICA

Olá!  Galerinha, que tal lembrarmos o que estudamos na aula de matemática...

 

COMBINAÇÃO DE OBJETOS

Combinando objetos através do princípio fundamental da contagem.

Podemos determinar o número de combinações entre objetos utilizando a Matemática, através do princípio fundamental da contagem. Por exemplo, vamos supor que Paulo tenha separado 5 camisetas, 3 calças, 3 pares de meia e 2 pares de tênis, pensando em ir à festa de aniversário de seu primo. De quantas maneiras possíveis Paulo poderá se vestir?

 

A combinação utilizada por Paulo envolverá 1 camiseta, 1 calça, 1 par de meia e 1 par de tênis. Nesses casos, para descobrirmos o número de opções possíveis, devemos multiplicar as quantidades de cada item. Observe:

 

5 x 3 x 3 x 2 = 90 combinações

 

Ao realizarmos a multiplicação, observamos que podemos ter 90 possíveis combinações.

 

Em uma lanchonete existem 4 tipos de sanduíche, 3 tipos de refrigerante, 5 tipos de sorvete e 2 tipos de brinde. Quantas combinações de lanches poderão ser informadas no cardápio de modo que envolva: 1 sanduíche, 1 refrigerante, 1 sorvete e 1 brinde?

 

4 x 3 x 5 x 2 = 120 combinações

 

No cardápio poderão ser informadas 120 combinações de lanche.

Adição;

Subtração;

Multiplicação e

Divisão;

Termos das quatro operações

·         Adição: 2 + 5 = 7 (2: parcela; 5: parcela; 7: soma ou total)

·         Subtração: 7 - 3 = 4 (7: minuendo; 3: subtraendo; 4: resto ou diferença)

·         Multiplicação: 4 x 2 = 8 (4: fator ou multiplicando; 2: fator ou multiplicador; 8: produto)

·         Divisão: 6 : 3 = 2 (6: dividendo; 3: divisor; 2: quociente)

Olá galerinha! Vocês sabiam que, quando estamos resolvendo uma continha de adição, subtração, multiplicação ou divisão, nós mesmos podemos descobrir se a conta está certa ou não? Isso mesmo, você pode corrigir suas continhas sozinho!

As operações matemáticas que realizamos possuem uma característica muito importante, cada uma delas possui uma operação inversa. É como se pudéssemos resolver a continha de trás para frente. Essas operações inversas são chamadas de prova real. Que tal conhecer algumas delas?

1°) Prova real da Adição

A operação inversa da adição é a subtração, logo a prova real da adição é a subtração. Pela soma de duas parcelas quaisquer, obtemos um resultado, e para conseguir a prova real, é necessário subtrair uma das parcelas do resultado da adição e obter a outra parcela como resultado. Vamos ver um exemplo:

2°) Prova real da Subtração

Se a subtração é a operação inversa da adição, logo a adição é a inversa da subtração. Para chegar à prova real da subtração, é necessário somar a segunda parcela com o resultado da subtração e obter a primeira parcela da subtração como resultado. Veja mais exemplos:

3°) Prova real da Multiplicação

A operação inversa da multiplicação é a divisão. Para chegar à prova real da multiplicação, é preciso dividir o resultado da multiplicação por qualquer uma de suas parcelas e obter a outra parcela. Observe como pode ser feita a prova real da multiplicação no exemplo a seguir:

 

 

4°) Prova Real da Divisão

Se a divisão é a operação inversa da multiplicação, então a multiplicação é a operação inversa da divisão. Para tirar a prova real da divisão, é necessário multiplicar o quociente pelo denominador, e o produto obtido deve ser igual ao dividendo. Observe alguns exemplos:

 

 

 

 

Encontre o resto da divisão, se houver.

 

As figuras geométricas espaciais possuem três dimensões (largura, altura e comprimentos) e são divididas em dois grupos: poliedros e corpos redondos.

Os poliedros são formados por arestas (segmentos de retas), vértices (o encontro de dois segmentos de retas) e faces (lado da forma geométrica espacial). Alguns exemplos de poliedros são: cubo, paralelepípedo, pirâmide, entre outros.

Os corpos redondos, por sua vez, possuem superfícies curvas; logo, não possuem faces laterais. Eles também podem ser chamados de sólidos de revolução, haja vista que são formados pela rotação de uma figura plana (figura geradora) ao redor de seu eixo – entenda rotação como dar uma volta completa. São corpos redondos: o cone, a esfera e o cilindro.

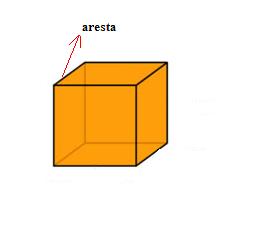
Arestas são as linhas resultantes do encontro de duas faces. Ou seja, quando duas faces se encontram elas formam uma linha e essa linha é chamada de aresta.

 

O cubo possui 12 arestas.

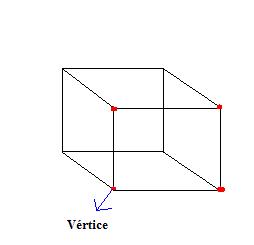
Vértices são os pontos de encontro das arestas. Ou seja, arestas de um poliedro se encontram em um ponto e esse ponto é o vértice do poliedro.

Pela figura podemos ver que o cubo possui 8 vértices.

Podemos fazer uma pequena tabela com os elementos do cubo:

O Plano Cartesiano é definido por duas retas perpendiculares. Por meio dele, é possível encontrar localizações no plano, calcular a distância entre dois pontos, distâncias entre ponto e reta, entre outros. Existem inúmeras utilidades para o plano cartesiano. Uma das mais importantes é relacionar a Geometria com a Álgebra, dando origem à disciplina conhecida como Geometria Analítica.

Retas numéricas no plano cartesiano

As duas retas que constituem o plano cartesiano são retas numéricas que se encontram na origem. Isso significa que cada uma dessas retas é associada aos números reais. Em outras palavras, qualquer ponto destacado em uma dessas retas representa um único número real. O fato de se encontrarem na origem significa que elas compartilham o ponto referente ao número real zero. Como o ângulo entre elas tem que ser de 90°, seu desenho será o seguinte:

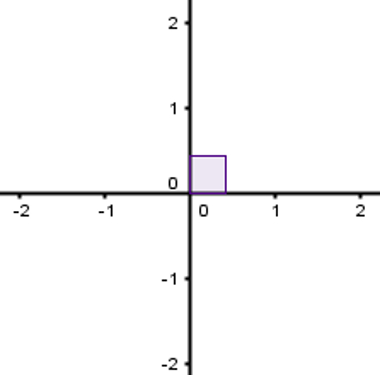
Duas retas perpendiculares que se encontram na origem

Observe que os sentidos positivos dessas retas foram escolhidos: para cima, na reta vertical, e para a direita, na reta horizontal. Esse sentido é extremamente importante para determinar corretamente localizações no plano.

Bons Estudos….