REVISÃO DE MATEMÁTICA FLORESTA P2

 Revisão de matemática Floresta P2

Olá galerinha!

Jamais considere seus estudos como uma obrigação, mas como uma oportunidade invejável para aprender a conhecer a influência libertadora da beleza do reino do espírito, para seu próprio prazer pessoal e para proveito da comunidade à qual seu futuro trabalho pertencer. – Albert Einstein

 

TIPOS DE ÂNGULOS E COMO USAR O TRANSFERIDOR.

 

Ângulos são duas semirretas que têm a mesma origem, no vértice, e são medidos em grau (º) ou em radiano (rad), de acordo com o Sistema Internacional.

Tipos de Ângulos

Conforme as suas medidas, os ângulos são classificados em agudo, reto, obtuso e raso.

Agudo

O ângulo agudo mede menos do que 90º

Reto

O ângulo reto mede o mesmo que 90º ( = 90º).

Obtuso

O ângulo obtuso mede mais do que 90º e menos do que 180º 

Raso

O ângulo raso, também conhecido como meia volta, mede o mesmo que 180º 

Perímetro é a medida do comprimento de um contorno.

Observe um campo de futebol, o perímetro dele é o seu contorno que está de vermelho.



Para fazermos o cálculo do perímetro devemos somar todos os seus lados:

P=100+70+100+70
P = 340 m

O perímetro da figura é a soma de todos os seus lados:

P = 10 + 8 + 3 + 1 + 2 + 7 + 2 +3

P = 18 + 4 + 9 + 5

P = 22 + 14

P = 36

 

1) Pedro foi à casa de Bianca e ficou admirado com o tamanho de sua piscina, por esse motivo perguntou quais eram as dimensões, ela respondeu que possuía 5m de largura, 7m de comprimento e 2m de profundidade. De acordo com as dimensões fornecidas por Bianca, calcule o perímetro da piscina

 

A piscina possuí o formato retangular. Para calcular o seu perímetro utilizaremos somente as medidas referentes à largura e comprimento. Sendo assim, o perímetro da piscina é:

 

P = 5 m + 5 m + 7 m + 7 m
P = 24 m

 

A borda da piscina, ou seja, seu perímetro, mede 24 m.

2) Observe a planta de um apartamento e calcule o seu perímetro em metros.

 

É possível notar na imagem que nem todas as unidades de medida são as mesmas. Quando isso acontece devemos fazer a transformação dessas unidades. Neste exercício todas as unidades de medida devem ser o metro (m).

 

4,5 m = 4,5 m
1,5 m = 1,5 m
300 cm = 3 m
5 m = 5 m
200 cm = 2 m
180 cm = 1,8 m
1,2 m = 1,2 m
150 cm = 1,5 m
140 cm = 1,4 m
110 cm = 1,1 m

P = 4,5 m + 1,5 m + 3 m + 5 m + 2 m + 8 m + 1,5 m + 1,5 m + 1,1 m
P = 23 m

O perímetro do apartamento é 23 m.

 

Área

Área é a medida de uma superfície.

A área do campo de futebol é a medida de sua superfície (gramado).

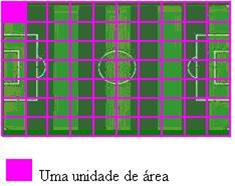
Se pegarmos outro campo de futebol e colocarmos em uma malha quadriculada, a sua área será equivalente à quantidade de quadradinho. Se cada quadrado for uma unidade de área:


Veremos que a área do campo de futebol é 70 unidades de área.

A unidade de medida da área é: m² (metros quadrados), cm² (centímetros quadrados), e outros.

Não esqueça que para calcular a área é: Base x Altura.

 

 

Vamos entender o que é Possibilidade e probabilidade:

Possibilidade é algo que pode acontecer, mas não é certeza.

Quando dizemos: Pode ser que chova hoje! Há possibilidade de chuva, mas não é certeza que vai chover.

Imagine que você jogou uma moeda para cima, nesse caso há duas possibilidades, ela pode cair do lado cara ou coroa, a cara seria a efígie da República ou o "homenageado" e a coroa, o lado do valor.

A mesma ideia para um jogo de dado: ao lançar um dado temos seis possibilidades para o lado que cairá para cima, como mostra a imagem.

Assim, podemos desenvolver nosso Raciocínio Combinatório que é a maneira de calcular o número total de possibilidades de um caso. Vamos lá!

Júlio tem três camisetas e três bonés de cores diferentes. Quais são as possibilidades de ele sair para passear sem repetir as peças?

Vamos raciocinar: Com cada camiseta ele pode usar três bonés diferentes; então multiplicaremos o número de camiseta vezes o número de bonés.

3 x 3 = 9 Possibilidades

Probabilidade, do mesmo jeito que a Possibilidade, é qualquer coisa que pode acontecer. Só que na Probabilidade tem-se uma estimativa de quanto pode e quanto não pode acontecer. No caso da moeda, por exemplo:

50% de sair cara
50% de sair coroa

Por que 50%? A probabilidade de sair coroa é uma de duas possibilidades. Representamos 1/2 = 0,5 Multiplicamos por 100 para obter o valor em porcentagem: 0,5 x 100 = 50

 

Vamos calcular a probabilidade: Ao atirar um dado, qual a probabilidade de sair o lado 5 voltado para cima?

O dado possui 6 lados, o lado 5 é uma possibilidade desses seis lados, então representamos pela fração 1/6 = 0,16 x 100 = 16%. A probabilidade de sair o lado 5 para cima é de 16%. Vamos calcular a probabilidade: Ao atirar um dado, qual a probabilidade de sair o lado 5 voltado para cima?

Sabendo que tenho 9 blusas no armário:

4 de cor azul

3 de cor amarela

2 de cor laranja

Qual a probabilidade de eu tirar a blusa laranja? A probabilidade é de 2 chances em 9 ou seja 22,22 %.

Pirâmides

As pirâmides são poliedros caracterizados por possuir uma base poligonal no plano e apenas um vértice fora do plano. Seu nome é representado pelo polígono que serve de base, os exemplos mais comuns são:

Uma fração é um número que representa a divisão entre dois números inteiros. As frações também representam uma ou muitas partes de um objeto que foi dividido em partes iguais. Vamos agora aprender como somá-las ou subtraí-las?

Adição e subtração de frações com denominadores iguais

Quando as frações a serem somadas tiverem denominador igual, o resultado será composto da seguinte maneira:

Numerador: Soma dos numeradores das frações;

Denominador: Repetir o denominador, que é igual em todas elas.

Por exemplo:

 7 + 9 – 3 = 7 + 9 – 3 = 16 – 3 = 13
 3    3    3           3              3         3 

Observe, no exemplo, que a subtração de frações de denominadores iguais segue o mesmo padrão da adição.

Operações com Números Decimais: Adição, Subtração, Multiplicação e Divisão

Para realizar as operações dos números decimais, devemos alinhar os números segundo a vírgula e as casas decimais que possuem.

Adição

Subtração

Multiplicação

Divisão

 

Os números decimais são números racionais (Q) não inteiros expressos por vírgulas e que possuem casas decimais, por exemplo: 1,54; 4,6; 8,9, etc. Eles podem ser positivos ou negativos.

As casas decimais são contadas a partir da vírgula, por exemplo o número 12,451 possui três casas decimais, ou seja, três algarismos após a vírgula.

 

Planificação do dado

 

Explicação passo-a-passo:

Dica:  o lado o oposto tem que dar sempre 7

Exemplo tem o cinco em cima e o dois em baixo e 5+2=7

 

PROVA REAL

 

Olá galerinha! Vocês sabiam que, quando estamos resolvendo uma continha de adição, subtração, multiplicação ou divisão, nós mesmos podemos descobrir se a conta está certa ou não? Isso mesmo, você pode corrigir suas continhas sozinho!

As operações matemáticas que realizamos possuem uma característica muito importante, cada uma delas possui uma operação inversa. É como se pudéssemos resolver a continha de trás para frente. Essas operações inversas são chamadas de prova real. Que tal conhecer algumas delas?

1°) Prova real da Adição

A operação inversa da adição é a subtração, logo a prova real da adição é a subtração. Pela soma de duas parcelas quaisquer, obtemos um resultado, e para conseguir a prova real, é necessário subtrair uma das parcelas do resultado da adição e obter a outra parcela como resultado. Vamos ver um exemplo:

 

 

2°) Prova real da Subtração

Se a subtração é a operação inversa da adição, logo a adição é a inversa da subtração. Para chegar à prova real da subtração, é necessário somar a segunda parcela com o resultado da subtração e obter a primeira parcela da subtração como resultado. Veja mais exemplos:

 

3°) Prova real da Multiplicação

A operação inversa da multiplicação é a divisão. Para chegar à prova real da multiplicação, é preciso dividir o resultado da multiplicação por qualquer uma de suas parcelas e obter a outra parcela. Observe como pode ser feita a prova real da multiplicação no exemplo a seguir:

 

 

 

4°) Prova Real da Divisão

Se a divisão é a operação inversa da multiplicação, então a multiplicação é a operação inversa da divisão. Para tirar a prova real da divisão, é necessário multiplicar o quociente pelo denominador, e o produto obtido deve ser igual ao dividendo. Observe alguns exemplos:

 

 

 

 

 

 

Encontre o resto da divisão, se houver.

 

 

 

 

 

Para verificar se a divisão está correta, faça:

D = d . q + r
D = 4 . 6 + 2
D = 26

Dividendo = 26; Divisor = 4; Resto = 2, Quociente = 6

 

O resto da divisão de 26 por 4 é 2; essa é uma divisão não exata então deverá ser somado quando for realizar a prova real. 

Bons estudos!

 

 

 

 

Dicas de como resolver situações Problemas

 

Dicas de como resolver situações Problemas

Os problemas matemáticos são responsáveis pelas inúmeras dúvidas presentes entre os alunos. A grande questão é relacionar as informações fornecidas com os símbolos matemáticos, adequados para a solução dos problemas. O aluno precisa entender a situação, identificando a operação mais adequada para a resolução, e isso depende de uma leitura segura e de um processo interpretativo. Através de exemplos, demonstraremos como realizar essa leitura interpretativa, selecionando as palavras-chave, bem como utilizando as operações adequadas.

Existem problemas matemáticos que utilizam, na sua resolução, equações e expressões numéricas. Trabalharemos agora com problemas que envolvem frações e veremos como aplicar a noção de inteiros e parte desses inteiros quando eles assumirem valores reais.

Veja alguns exemplos e as explicações passo a passo de como encontrar a solução desse tipo de problema e de como a fração pode ser encontrada em situações problemas.

Exemplo 1:

Em certo país, os trabalhadores recebem dois salários mínimos em dezembro: o salário normal e o 13º salário. Se a pessoa trabalhou os 12 meses do ano, os dois salários serão iguais. Se a pessoa trabalhou uma fração do ano, o 13º salário corresponderá a essa fração do salário normal. Se o salário normal de uma pessoa é 516 reais e ela trabalhou 7 meses nesse ano, quanto ela vai receber de 13º salário?

Resolução:
Esse trabalhador não trabalhou o ano inteiro, de 12 meses do ano ele trabalhou 7 meses. A fração que corresponde ao tempo que ele trabalhou é 7/12 . Como a situação problema informou que o valor recebido no 13º salário é a mesma fração do tempo trabalhado, podemos escrever que ele irá receber 7/12 do salário normal. Como o salário dele é 516 reais, para descobrir quanto ele irá receber no 13º salário, devemos encontrar:

7/12 de 516. Então 516 : 12 = 43 e 43 x 7 = 301.

Portanto, o salário que o trabalhador irá receber no seu 13º salário será de 301 reais que corresponde a 7 meses trabalhados durante o ano.

Exemplo 2:

João Carlos é operário e seu salário é de apenas 520 reais por mês. Gasta 1/4 com aluguel
 
e  2/5 com alimentação da família. Esse mês ele teve uma despesa extra:  3/8 do seu salário foram gastos com remédios. Sobrou dinheiro?

Resolução:
Para saber se o salário de João Carlos foi suficiente para pagar todas as suas despesas é preciso encontrar o valor que ele gastou com o pagamento do aluguel, com a alimentação e com os remédios. Então, veja:

1 de 520 = 520 : 4 x 1 = 130.
4

2 de 520 = 520 : 5 x 2 = 104 x 2 = 208
5

3 de 520 = 520 : 8 x 3 = 195.
8

Concluímos que ele gastou com essas despesas um total de 130+208+195 = 533 reais. Portanto, não sobrou nada de seu salário; pelo contrário, ele ficou devendo, pois suas despesas foram 13 reais a mais que seu salário.

 

Exemplo 3

Carlos comprou uma televisão no valor de R$ 950,00, dividida em 10 prestações iguais. Ao pagar a 4º prestação, recebeu de presente de seu avô, o restante do dinheiro para a quitação do aparelho. Quanto Carlos recebeu?

O valor do aparelho é igual a R$ 950,00.

Carlos resolveu dividir o televisor em 10 prestações iguais, então devemos realizar uma operação de divisão: 950: 10 = 95 reais.

Carlos efetuou o pagamento de 4 prestações, dessa forma, ainda faltam 6. São as prestações restantes que o avô de Carlos resolveu pagar. Portanto, 95 * 6 = 570 reais.

Carlos recebeu R$ 570,00 de seu avô.

REVISÃO DE GRAMÁTICA LP Floresta P2

 

REVISÃO DE GRAMÁTICA LP Floresta P2

 

Meus queridos alunos!

Tudo que vale a pena é difícil e exige esforço. Estudem mesmo sendo complicado, porque trará os melhores resultados.

 

 

 Pronomes pessoais

Os pronomes pessoais indicam as pessoas gramaticais, também chamadas de pessoas do discurso (Eu, tu, ele, nós, vós, eles). Eles podem pertencer ao caso reto e ao caso oblíquo. Para cada pronome reto, há um correspondente no caso oblíquo. Veja a explicação!

 

Eu →Me, mim, comigo.

Tu → Te, ti, contigo.

Ele → Se, o, a, lhe, si, consigo.

Nós→ Nos, conosco.

Vós →Vos, convosco.

Eles →Se, os, as, lhes, si, consigo.

 

Os pronomes interrogativos são aqueles que utilizamos nas construções de perguntas diretas ou indiretas: que, quem, qual, quanto. Cada um desses vocábulos possui um valor e um uso específico na construção do enunciado. Veja!

·         Pronome QUE

a) pode ser um pronome substantivo quando carregar o significado de “que coisa”.

Que foi feito daquela mesa?

b) pode ser um pronome adjetivo quando carregar o significado de “que espécie de”.

Que animal é aquele?
Que atitude foi essa?

Observação: O sentido do pronome QUE, pronome substantivo, pode ser intensificado quando são usadas as expressões o que, que é que, o que é que e que é o que:

O que foi feito daquela mesa?
O que é que foi feito daquela mesa?

·         Pronome QUEM

Esse pronome refere-se apenas a pessoas ou coisas personificadas.

Quem revelou o crime?
Diga-me quem disse tal coisa.

·         Pronome QUAL

Esse pronome carrega um sentido de seletividade, ou seja, é aquele que faz uma seleção de uma pessoa ou coisa na construção da pergunta. Normalmente, ele possui a função de pronome adjetivo.

Qual dos filmes você prefere?
Não sei qual filme prefiro.

Observação: É possível intensificar a ideia de seletividade desse pronome utilizando-se a expressão qual dos (das, de):

Qual dos filmes você prefere?
Não sei qual dos filmes prefiro.

·         Pronome QUANTO

Esse pronome refere-se à ideia de uma quantidade indefinida. Ele pode exercer a função de pronome substantivo ou pronome adjetivo.

Quantos irmãos você tem?
Diga-me quantos irmãos você tem.

 

Verbo é a palavra que exprime um fato, localizando-o no tempo. Geralmente exprime ideia de ação, estado ou fenômeno.

É importante ressaltar que os verbos podem expressar outros tipos de fatos que não ação, estado ou fenômeno. Observe o exemplo abaixo:

Sou eu que faço você sofrer?
Ou é você que sofre por minha causa?

 

Os substantivos podem ser:

• Primitivos

Quando não são formados a partir de outra palavra. Exemplo: Livro

·         Derivados

Formados a partir de outra palavra. Exemplo: Livraria

·         Simples

Nomes que possuem apenas uma palavra. Exemplo: Chuva

·         Compostos

Nomes formados por duas palavras. Exemplo: Guarda-chuva

·         Concretos

Quando sua existência é independente, ou seja, não precisa de algo ou de alguém para se manifestar. Exemplo: Mesa

·         Abstratos

Quando sua existência depende de algo ou de alguém. Exemplo: Raiva

·         Coletivos

Quando indicam coleção, conjunto de seres, desde que pertençam à mesma espécie. Exemplo: Fauna (animais de uma região)

·         Comum

Quando não especificam, pelo contrário, generalizam. Exemplo: menino.

·         Próprio

Quando especificam, quando particularizam. Exemplo: João.

 

Substantivos:

Muitas são as classificações, mas o que define uma palavra como substantivo? Sua capacidade de nomear. Pense em uma palavra. Analise. Serve para quê? Para dar nome? Então é substantivo. Cadeira, mesa, bolsa, quadro, agenda, livro, computador, calendário, amor, enfim, nomeou, é substantivo.

O que é adjetivo?

O adjetivo é uma classe de palavras que atribui características aos substantivos, ou seja, ele indica suas qualidades e estados.

Essas palavras variam em gênero (feminino e masculino), número (singular e plural) e grau (comparativo e superlativo).

Exemplos de adjetivos:

·       garota bonita

·       garotas bonitas

·       criança obediente

·       crianças obedientes

 

Grau comparativo

No grau comparativo é feita a comparação da mesma característica em dois ou mais seres ou de duas ou mais características do mesmo ser.

Grau comparativo de inferioridade

Grau comparativo de inferioridade = menos (adjetivo) que/do que

• Alice é menos preguiçosa que João.
• A revista é menos pesada do que o livro.

Grau comparativo de igualdade

Grau comparativo de igualdade = tão (adjetivo) quanto/ como/ quão

• Cláudia é tão educada como Patrícia.
• Matemática é tão importante quanto português.
• Ele é tão decidido quão teimoso.
• Marcia é tão inteligente quanto Maria

 

Grau comparativo de superioridade

Grau comparativo de superioridade = mais (adjetivo) que/ do que

• Igor é mais atento que Rodrigo.
• O lápis é mais comprido do que a borracha.
• A minha professora de matemática é mais legal que a sua.

Grau superlativo

No grau superlativo é feita a caracterização de um ou mais seres, atribuindo qualidades em grau muito elevado ou em maior ou menor grau que os demais seres.

Grau superlativo absoluto sintético = adjetivo + sufixo (-íssimo; -imo; - ílimo; -érrimo)

• A sobremesa é dulcíssima.
• O teste foi facílimo.
• O professor é sapientíssimo.
• Chegamos da viagem cansadíssimos

 

Comprimento e cumprimento.

Existem algumas palavras na língua portuguesa que sempre causam problema para um falante distraído. Isso, geralmente, acontece com os PARÔNIMOS, que são aquelas palavras muito parecidas na escrita e na pronúncia, mas que querem dizer coisas bem diferentes.

Quem, por exemplo, nunca se engasgou na hora de empregar as palavras COMPRIMENTO e CUMPRIMENTO.

Você diria que: A costureira marcou o cOmprimento ou o cUmprimento do vestido?

Certamente, a costureira marcou o COMPRIMENTO, o tamanho do vestido. A palavra COMPRIMENTO tem o sentido de dimensão, tamanho, extensão.

Já CUMPRIMENTO tem o sentido de saudar alguém, de cumprimentar uma pessoa.

Dizemos que foi amistoso o CUMPRIMENTO entre o presidente e o senador.

A palavra cumprimento também pode derivar do verbo CUMPRIR que quer dizer executar.

Assim podemos dizer que o delegado estava no CUMPRIMENTO de suas funções.

Estamos o uso do Há e o a

Existem algumas palavras da nossa língua que só dão problema na hora de escrever. Isso acontece muito com as palavras têm o mesmo som, mas grafia e significado diferentes.

Os exemplos de casos em que isso acontece são muitos, mas hoje vamos nos concentrar numa duplinha que nos atormenta: a diferença entre HÁ com agá e A sem agá.

A dica mais importante para entender a diferença entre eles é lembrar que HÁ com agá é verbo (forma do verbo HAVER) e por isso pode ser substituído por outro verbo.

Assim, devemos escrever com agá:

“Há dúvidas na prova”.

Nesse caso, podemos substituir o HÁ pelo verbo existir: “Existem dúvidas na prova”.

Na frase “Há muito tempo não o vejo”, também é com agá, pois podemos dizer: “Faz tempo que não o vejo”.

Já na frase “Estamos a dois minutos de casa”, o A deve ser escrito sem agá, pois não pode ser substituído por um verbo. Não tem sentido dizer: "Estamos faz dois minutos de casa" ou "Estamos existem dois minutos de casa".

Trata-se da preposição “A”. Podemos usar quando nos referimos à distância ou a tempo futuro: “Estamos a vinte quilômetros do aeroporto”, “Ele chegará ao trabalho daqui a dez minutos”.

 

Mal é o contrário de bem e Mau é o contrário de bom 

 

Mal e mau são palavras antônimas - possuem o significado oposto em comparação à outra. No caso de mal com “l”, a palavra antônima será bem. Para utilizar a palavra mal de forma correta é necessário ficar atento ao seu significado contrário. 

Mal também pode ser sinônimo de inadequadamente, ilegalmente, desarmoniosamente, erradamente, defeituosamente, incorretamente, irregularmente, entre outros. A palavra mal se origina da palavra “male” em latim. 

Mau

Mal e mau também são palavras homófonas, que possuem a mesma fonética mesmo possuindo grafias diferentes. O mau com “u” também é uma palavra antônima. Neste caso, a palavra antônima de mau será bom. Então para fazer uso de maneira correta, basta lembrar a palavra que é contrária a ela.

Mau também é sinônimo de malfeito, defeituoso, mal-acabado, ruim, imperfeito, desprimoroso, inferior, medíocre, ordinário, péssimo, reles, irregular, velho, estragado, horrível, atamancado, entre outros.

A palavra mau se origina da palavra “malu” em latim.

 

Classificação dos advérbios

Primeiramente, é importante entender que os advérbios modificam outras palavras e sua classificação serve para entender de que forma eles modificam essas palavras, quais sentidos serão adicionados. Assim, os exemplos a seguir não abordam todos os advérbios que existem, mas trazem os que são os mais comuns.

A classe gramatical dos advérbios é muito relacionada com os adjetivos e verbos.

 

·         Advérbios de lugar

São as palavras que indicam uma localização. Os advérbios de lugar mais comuns são aqui, ali, lá, atrás, perto, longe, dentro, fora, entre outros.

Veja:

• Meu amigo mora longe.
• Você pode vir aqui?
• O lugar fica atrás dessa casa.
• Meu gato estava no meio da rua

 

Advérbios de tempo

São as palavras que expressam tempo/período. Os advérbios de tempo mais comuns são hoje, amanhã, ontem, sempre, nunca, antes, depois, cedo, tarde, entre outros.

Veja:

• Eu cheguei depois.
• Nós fomos ontem.
• O evento acabará cedo.
• Ontem minha prima viajou.

 

Advérbios de modo

São as palavras que ajudam a entender o modo/a maneira como alguma ação ocorreu ou como ocorre alguma característica. Os advérbios de modo mais comuns são bem, mal, melhor, pior, vagarosamente, rapidamente, entre outros. Também é possível transformar muitos adjetivos em advérbio de modo acrescentando o sufixo -mente ao final da palavra.

Veja:

• Você acabou rapidamente.
• Tudo ficará melhor.
• Vocês escrevem perfeitamente.
• Suas tarefas eram bem completas.
• Ela era naturalmente cacheada.
• Julia atendeu o cliente educadamente.

 

Advérbios de intensidade

São as palavras que ajudam a entender o quão intensa é a ação do verbo ou a característica do adjetivo. Os advérbios de intensidade mais comuns são muito, pouco, demais, bastante, mais, menos, entre outros.

Veja:

• Você quer mais suco?
• Façam menos barulho.
• Ela está meio cansada.
• Nós éramos bastante quietos.
• Corríamos muito rapidamente.
• Os alunos estavam bastante interessados na aula de hoje.

 

Advérbios de afirmação

São as palavras que complementam ou reforçam o sentido de afirmação. Os advérbios de afirmação mais comuns são sim, certamente, realmente, entre outros.

Veja:

• O jurado criticou positivamente nosso trabalho.
• Eu certamente tirarei férias em breve.

 

Advérbios de negação

São as palavras que complementam ou reforçam o sentido de negação. Os advérbios de negação mais comuns são não, nunca, jamais, entre outros.

• Não fizeram questão da nossa presença.
• Cláudio jamais faria uma coisa assim.
• Não dê importância ao que os outros dizem.

 

Advérbios de dúvida

São as palavras que dão a ideia de dúvida. Os advérbios de dúvida mais comuns são talvez, provavelmente, eventualmente, quiçá, porventura, entre outros.

• Provavelmente, sairemos ao anoitecer.
• Talvez essa não seja a melhor escolha.

 

Locuções adverbiais

As locuções adverbiais seguem exatamente a mesma lógica dos advérbios. Porém, elas chamam-se locuções adverbiais, porque são duas ou mais palavras juntas para passarem as ideias que vimos anteriormente nos advérbios, além de outros sentidos.

Locuções adverbiais de lugar: ao redor, por perto, em cima, por ali, à esquerda, entre outros.

Locuções adverbiais de tempo: logo mais, em breve, de manhã, mais tarde, para sempre, nunca mais, entre outros.

Locuções adverbiais de modo: bem devagar, ao contrário, em detalhes, entre outros.

Locuções adverbiais de intensidade: em excesso, de todo, muito menos, bem maior, entre outros.

Locuções adverbiais de afirmação: com certeza, de fato, sem dúvidas, entre outros.

Locuções adverbiais de negação: de jeito nenhum, nunca mais, de maneira nenhuma, entre outros.

Locuções adverbiais de dúvida: quem sabe, entre outros.

Diferenças entre advérbios e adjetivos                   

Para não confundir advérbio com adjetivo, lembre-se: o advérbio complementa o sentido do verbo, do adjetivo ou de outro advérbio, enquanto o adjetivo complementa o sentido do substantivo. Por exemplo:

Você é delicado.
“Delicado” é uma característica do sujeito, portanto, é adjetivo.

Você age delicadamente.
“Delicadamente” é a maneira como o sujeito age, portanto, é advérbio (de modo).

 

Adjetivos Pátrios são aqueles que caracterizam as pessoas ou as coisas de acordo com as suas origens, considerando países, continentes, cidades, regiões, entre outros.

Os adjetivos pátrios devem ser grafados com letras minúsculas.

 

São Paulo – paulista

Rio de Janeiro – fluminense

Bahia - baiano (sem h)

Minas Gerais – mineiro ou geralista

Palmas - palmense

Florianópolis - florianopolitano

Belém - belenense

 

França – francês

Estados Unidos da América – estadunidense ou americano

Holanda – holandês

Inglaterra - inglês, anglo, anglo-saxão ou britânico

Brasil- brasileiro

Noruega – norueguês

 

Masculino e feminino

As coisas, assim como pessoas, animais, objetos, comidas, têm nome. Esses nomes são chamados de substantivos e aparecem em gêneros diferentes, o masculino e o feminino.

Conforme o gênero de cada coisa, usamos os artigos. “o - um” para masculino e “a - uma” para feminino. É como se estivéssemos definindo o sexo de tudo.

A palavra relógio é acompanhada de “o ou um”.                

Exemplos: - O relógio do meu irmão caiu e quebrou.
                     - Um relógio de ouro é muito caro.

O mesmo acontece com as palavras do gênero feminino.

Exemplos: - A boneca é conhecida no mundo todo.
                    - Uma menina ganhou o concurso de redação.

Observe como os artigos variam de acordo com o gênero do substantivo:

A palavra chinelo é do gênero masculino, portanto deve ser acompanhada de artigo masculino, o chinelo. Muitas pessoas falam como se a palavra fosse feminina, “a chinela”, mas essa forma de falar é errada.

Existem palavras que comportam os dois gêneros, tanto no masculino como no feminino. Então usa-se “o - um” e “a - uma”, como no caso da palavra caneca.

Exemplo: - A caneca de leãozinho é a minha preferida.
                  - Meu pai toma chocolate quente em um caneco grande.

Algumas palavras podem mudar de gênero, leia o quadro e observe:

Outras palavras não variam no gênero, aparecendo da mesma forma para o masculino e para o feminino, como no caso de algumas espécies animais, aparecendo como machos e fêmeas. Exemplos: peixe macho - peixe fêmea; cobra macho – cobra fêmea; grilo macho – grilo fêmea; pássaro macho – pássaro fêmea; baleia macho – baleia fêmea; aranha macho – aranha fêmea, etc.

 

Mais ou mas: dica básica

Para entender melhor, nós criamos dicas básicas para você saber a diferença do uso do mais e do mas. É bastante simples:

• mas – é usado para dar ideia de oposição e contrariedade
• mais – é indicativo de quantidade e intensidade

 

Uso dos porquês

Assim, quando a palavra for escrita junta e sem acento, seu valor semântico será de “pois”, “uma vez que” e possuirá a função sintática de conjunção causal ou explicativa. Esses critérios (semânticos e sintáticos) determinam o uso dos diferentes porquês em língua portuguesa. Vamos analisá-los detalhadamente a seguir:

• PORQUE: é uma conjunção causal ou explicativa, podendo ser substituída por “pois”, “uma vez que”.

Exemplo:

Estude, porque as provas serão na próxima semana.

• PORQUÊ: é um substantivo, podendo ser acompanhado de artigo, pronome, adjetivo ou numeral.

Exemplo:

Não sabia o porquê de tanta ansiedade.

• POR QUE: (1) é a junção da preposição por + pronome interrogativo e inicia perguntas diretas ou está presente no interior de perguntas indiretas, podendo ser substituído por “por qual razão” ou “por qual motivo”. (2) é a junção da preposição por + pronome relativo e terá o significado de “pelo qual” e suas flexões.

Exemplos:

Quero saber por que você não atende meus telefonemas.

Os lugares por que viajei são inesquecíveis.

• POR QUÊ: é a junção da preposição por + pronome interrogativo. Aparecerá sempre no final de uma frase, podendo ser substituído por “por qual motivo”, “por qual razão”.

Exemplos:

Você parece triste, por quê?

Ela está chorando sem saber por quê.

Agora e com vocês! Não esqueça de fazer questionários com perguntas e respostas.

 

Bons estudos!